| Главная » Статьи » Математика » Алгебра |
Четные и нечетные функции.
Будем рассматривать функции, области определения которых симметричны относительно начала координат. Это означает, что для любого x из области определения, число -x так же принадлежит области определения. Среди таких функций можно выделить два особых класса - четные функции и нечетные функции. Определение: Функция f называется четной, если для любого x из области определения f(-x) = f(x). График произвольной четной функции приведен на рисунке ниже. 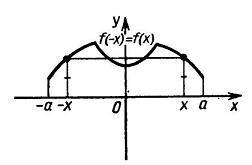 Определение: Функция f называется нечетной, если для любого x из области определения f(-x) = -f(x). График произвольной четной функции приведен на рисунке ниже. 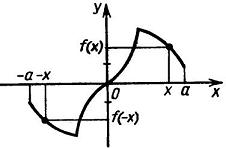 Следует отметить, что помимо четных и нечетных функций, встречаются так же функции ни четные, ни нечетные. | |
| Просмотров: 555 | |
| Всего комментариев: 0 | |