| Главная » Статьи » Математика |
| В разделе материалов: 20 Показано материалов: 11-20 |
Страницы: « 1 2 |
Понятие о среднемЕсли дан ряд величин, то всякая величина, заключённая между наибольшей и наименьшей из данных величин, называется «средней». В математике наиболее распространены следующие средние. |
Отношения между числамиДля того чтобы найти некоторую часть числа, нужно это число умножить на дробь, выражающую эту часть. Пример 1 Найти Имеем 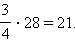 |
Иррациональные числаОказывается, что для нужд самой математики как, впрочем, и для практики, уже введённых рациональных чисел не хватает. Исторически числа, отличные по своей природе от рациональных, впервые появились уже при желании вычислить диагональ квадрата по его стороне. |
|
|
Обыкновенные дробиМожно еще больше расширить числовое множество – так, чтобы операция деления над натуральными числами была выполнима всегда. Для этого введем понятие дроби. |
Целые числаТеперь, когда у нас уже определены положение натуральных чисел на координатной прямой и число 0, мы можем расширить числовое множество так, чтобы операция вычитания была определена на всем множестве. |
Так, 3 ≡ 1 (mod 2), 7 ≡ 1 (mod 3). Два числа сравнимы по модулю 2, если они оба четны, либо если они оба нечетны. По модулю 1 все целые числа сравнимы между собой. В том случае, если число Свойства сравнений по модулю вытекают из свойств арифметических операций. | |||||||||
Понятие натуральных чиселПонятия «число» и «операция» не так просты, как это может показаться с первого взгляда. Почему, пользуясь одними и теми же числами, мы можем считать камушки и звезды? Это позволяет нам думать, что, сколько бы ни было объектов, мы всегда сможем их пересчитать, и операции сложения, умножения будут также применимы к ним. Подобные вопросы ставились и древними греками, и в наше время. В этом курсе мы будем исходить из того, что умение считать и различать разные количества предметов – врожденные способности человека. Возьмем в руки камушки, как это делали пифагорейцы, будем прибавлять их по одному, называть последовательно каждое количество своим именем и таким «наглядным» способом определим сразу два основных для алгебры понятия – число и операцию увеличения на единицу. Повторяя эту процедуру и предполагая, что ничто не мешает нам делать это бесконечно, мы сможем определить сложение и умножение на бесконечном множестве натуральных чисел. |
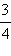 от 28.
от 28.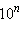 , может быть записана в виде
, может быть записана в виде